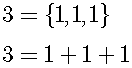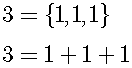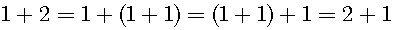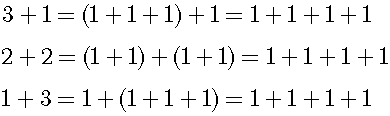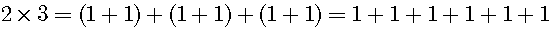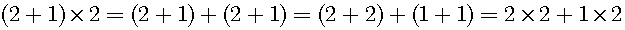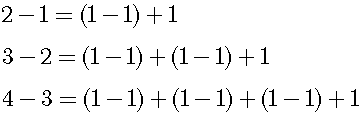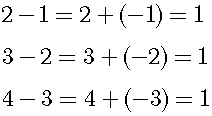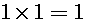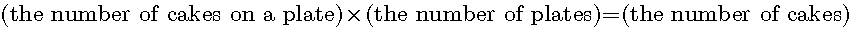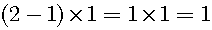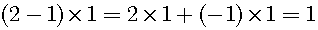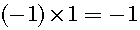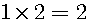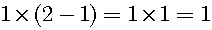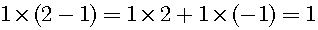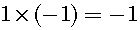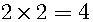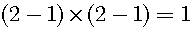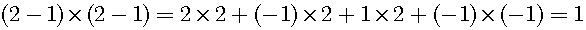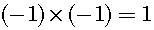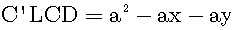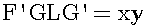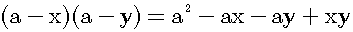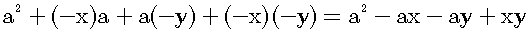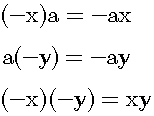Why is a negative times a negative a positive? This question is usually difficult to answer. So, I cannot find the satisfactory answer on the internet. I think that the correct answer has to be derived from the concept of
the natural number one.
We shall begin with the cardinal number. In "
The Concrete Basis of the Number Theory", I claim that the cardinal number can be represented by two forms:
We can easily derive the calculation rules from the second form.
The Calculation Rules
We can easily attain the associative law based on the second form of the cardinal number. Subsequently, the communicative law can be easily attained.
This definition is sufficient for natural numbers. Next, let us consider the distribution law. If we accept this definition, the distribution law is naturally obtained:
I think that the negative cardinal number does not exist. Obviously, the negative number of lives or humans does not exist. Also, the negative number of objects does not exist. For this reason, we must not accept the existence of negative cardinal numbers. In contrast to this, we are routinely using negative ordinal numbers. The Gregorian calendar and the Celsius temperature scale are well known examples. The Gregorian calendar was made based on the Christ birth as the reference zero. In this calendar, BC is identical to the negative. Together with this, the Celsius temperature scale is determined based on the freezing point of water as the reference zero. Another reference is the boiling point as 100. The interval between two reference points is divided into 100 degrees. In the Celsius scale, the negative temperature is common. These negatives are ordinal numbers based on the reference zero.
It should be noted that we can choose any point as the reference zero. However, the reference zero is different from the true zero. In the case of the temperature, the absolute zero is -273.16℃ on the Celsius scale. The lower temperature than absolute zero is impossible. If we choose the absolute zero as the reference point, the negative temperature does not exist. For the calendar, if time begins at the big bang, time did not exist until then. If we choose the moment of the big bang as the reference point, the negative time does not exist. Like these examples, if we select the true zero, negative numbers do not exist. In conclusion, negative numbers are assumed numbers.
The Subtraction and the Negative Number
In the concrete basis of the number theory, I defined the subtraction as the comparison of two numbers using one-to-one correspondence.
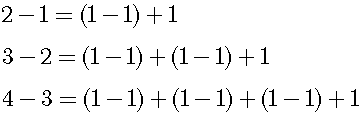
So, we define that addition of the negative number is identical to the subtraction of the same absolute value positive number. for example:
Calculation Rules of Negative Numbers
We shall derive calculation rules of negative numbers using the concrete example. There is one cake on one plate. This situation is represented by the equation:
In the left-hand side of the equation, the front term represents the number of cakes on a plate and the back term represents the number of plates. The right-hand side of the equation is the sum of cakes.
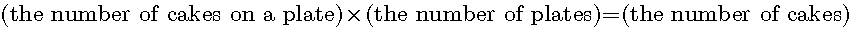
Next, let us consider a simple example. There are two cakes on one plate. If I take one cake from the plate, then one cake has been left.
The distribution law is applied to the above equation, just the same one cake has been left.
The difference between 2 and 1 is 1.
Next, let us consider another simple example. There are two plates. One cake is on each plate. There are two cakes.
If I take one plate, then one cake has been left.
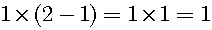
The distribution law is applied to the above equation, just the same one cake has been left.
The difference between 2 and 1 is 1.
Consequently, a negative times a positive is a negative and a positive times a negative is a negative. Next, let us consider the more complex example, which is shown in figure 1.
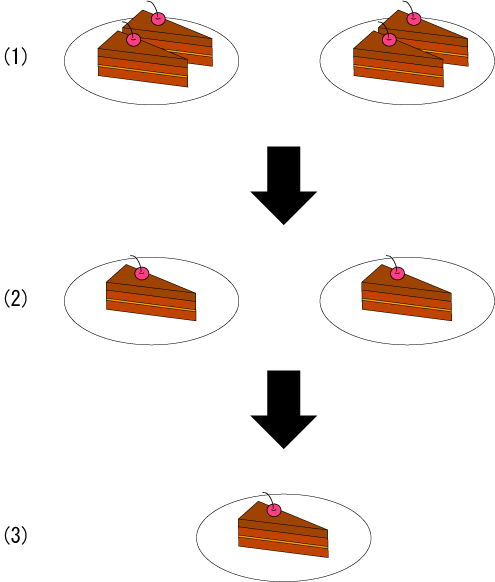 figure1
figure1
There are two plates. Two cakes are on each plate. The sum of cakes is four (figure 1-1).
Subsequently, if I take one cake from each plate, then two cakes have been left (figure 1-2). Subsequently, if I take one plate, then one cake has been left (figure 1-3).
The distribution law is applied to the above equation, just the same one cake has been left.
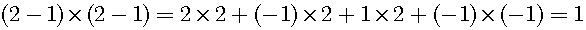
The above equation means:
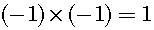
Therefore, a negative times a negative is a positive.
The Geometric Proof
The second meaning of the multiplication is the area. The area of the rectangle is height times width and the area of square is the square of a side. The irrational number is derived from this meaning of the multiplication. This meaning of the multiplication is important. So, using geometry, we have to prove that a negative times a negative equals a positive.
Figure 2 shows the square ABCD. The length of each side is a. The length of the line AE is x and the length of the line HC is y. The area of the yellow rectangle EFHD is (a-x)(a-y).
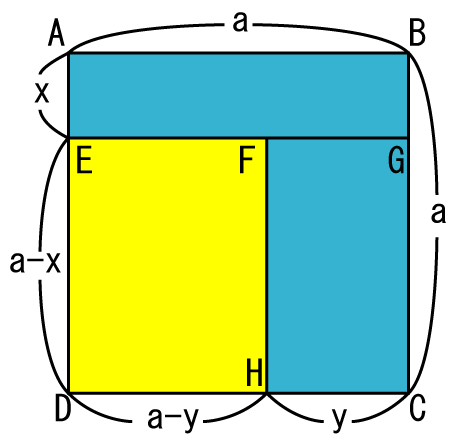 Figure 2
Figure 2Next, the light blue rectangle FGCH is moved to the position, in which the point H is on the point E and the line HF is on the line EG. The result is shown in figure 3.
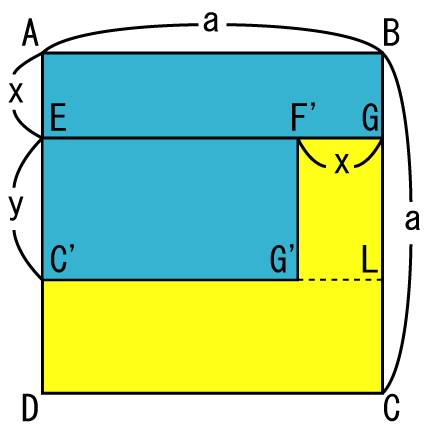 Figure 3
Figure 3 The yellow domain consists of the yellow rectangle C'LCD and the yellow rectangle F'GLG'. The area of the yellow rectangle C'LCD is the next equation:
The area of the yellow rectangle F'GLG' is the next equation:
The area of the yellow domain is equal to the yellow rectangle EFHD in figure 1. The next equation is obtained:
The distribution law is applied to the left-hand side of the equation.
Compare the left-hand side with the right-hand side of the equation.
The calculation rules of negative numbers are derived.
Table of Contents